Theory
Radian, a circle measure
One radian is the angle that an arc of 1 unit subtends at the centre of a circle of radius 1 unit.
Degrees to radians conversion: 1 degrees = π/180 radians
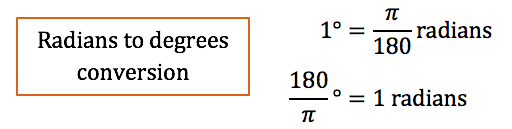
Radians and Degrees
π^c = 180°
where π^c = π radians
Relationship between radian measure and degrees
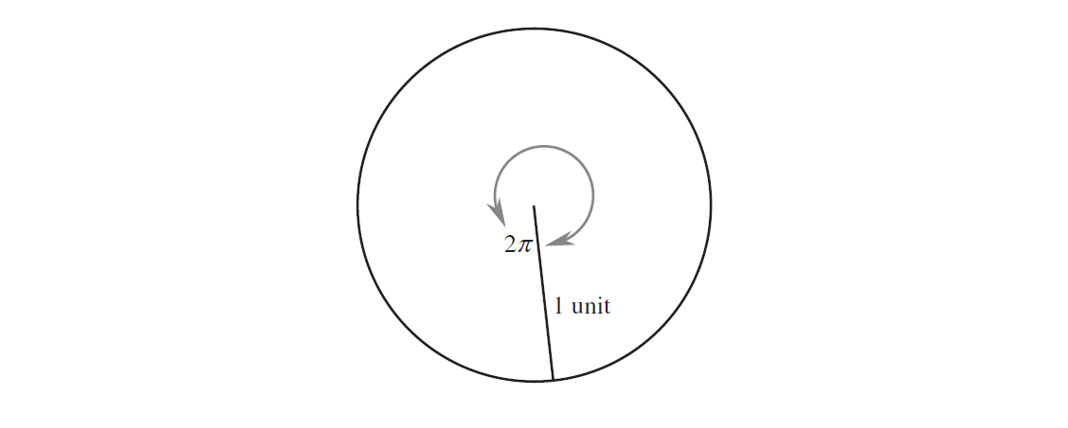
Circumference of the circle with radius 1 unit is given by:
C = 2πr
= 2π(1)
= 2π
T
The arc length of the whole circle is 2π.
∴ There are 2π radians in a whole circle.
But there are 360° in a whole circle (angle of revolution).
So 2π^c = 360°
π^c = 180°
Radians to Degrees
To change from radians to degrees: multiply by 180/π

Note: Special measure you will use regularly include -
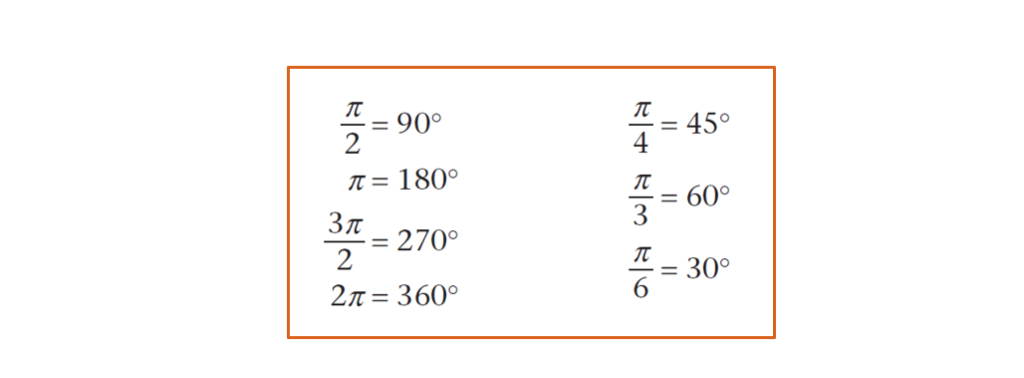
Practice Question
- Convert 5π/6 radians into degrees.
Solution
- To convert radians into degrees:
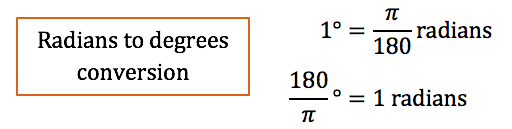
Therefore:
5π/6 radians = 180/π° x 5π/6
Simplyfying:
=900π/6π°
=150°



